如何使用git将项目代码上传到github
本文共 430 字,大约阅读时间需要 1 分钟。
如何用git将项目代码上传到github
1.准备GIT
参考我的博客下载Git 软件
2.身份认证
1.本地生成ssh信息
$ ssh-keygen -t rsa -C "your_email@youremail.com"
例如格式为:xxxx @ qq.com (这里直接一路回车按下去)
2.登录github打开SSH绑定界面
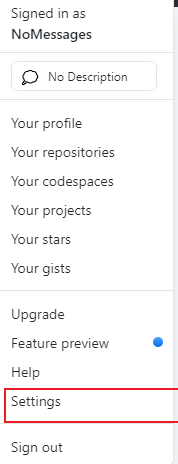
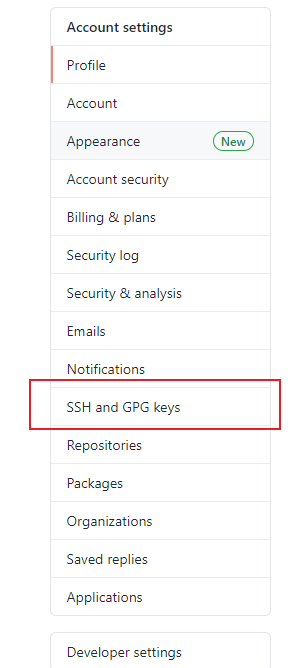
点击新增 将生成的ssh.pub中的内容复制进去即可

3.在git中绑定自己的信息
$ git config --global user.name "" //名称$ git config --global user.eamil "" //邮件
3.完成上传
其实在创建的时候,官网上已经说明如何操作了,

关键代码如下
$ git remote add origin 远端地址$ git add 需要提交的内容$ git commit . "提交"$ git push origin master 提交到远端
完成提交~
转载地址:http://bfspz.baihongyu.com/
你可能感兴趣的文章
mysql5.7 for windows_MySQL 5.7 for Windows 解压缩版配置安装
查看>>
Webpack 基本环境搭建
查看>>
mysql5.7 安装版 表不能输入汉字解决方案
查看>>
MySQL5.7.18主从复制搭建(一主一从)
查看>>
MySQL5.7.19-win64安装启动
查看>>
mysql5.7.19安装图解_mysql5.7.19 winx64解压缩版安装配置教程
查看>>
MySQL5.7.37windows解压版的安装使用
查看>>
mysql5.7免费下载地址
查看>>
mysql5.7命令总结
查看>>
mysql5.7安装
查看>>
mysql5.7性能调优my.ini
查看>>
MySQL5.7新增Performance Schema表
查看>>
Mysql5.7深入学习 1.MySQL 5.7 中的新增功能
查看>>
Webpack 之 basic chunk graph
查看>>
Mysql5.7版本单机版my.cnf配置文件
查看>>
mysql5.7的安装和Navicat的安装
查看>>
mysql5.7示例数据库_Linux MySQL5.7多实例数据库配置
查看>>
Mysql8 数据库安装及主从配置 | Spring Cloud 2
查看>>
mysql8 配置文件配置group 问题 sql语句group不能使用报错解决 mysql8.X版本的my.cnf配置文件 my.cnf文件 能够使用的my.cnf配置文件
查看>>
MySQL8.0.29启动报错Different lower_case_table_names settings for server (‘0‘) and data dictionary (‘1‘)
查看>>